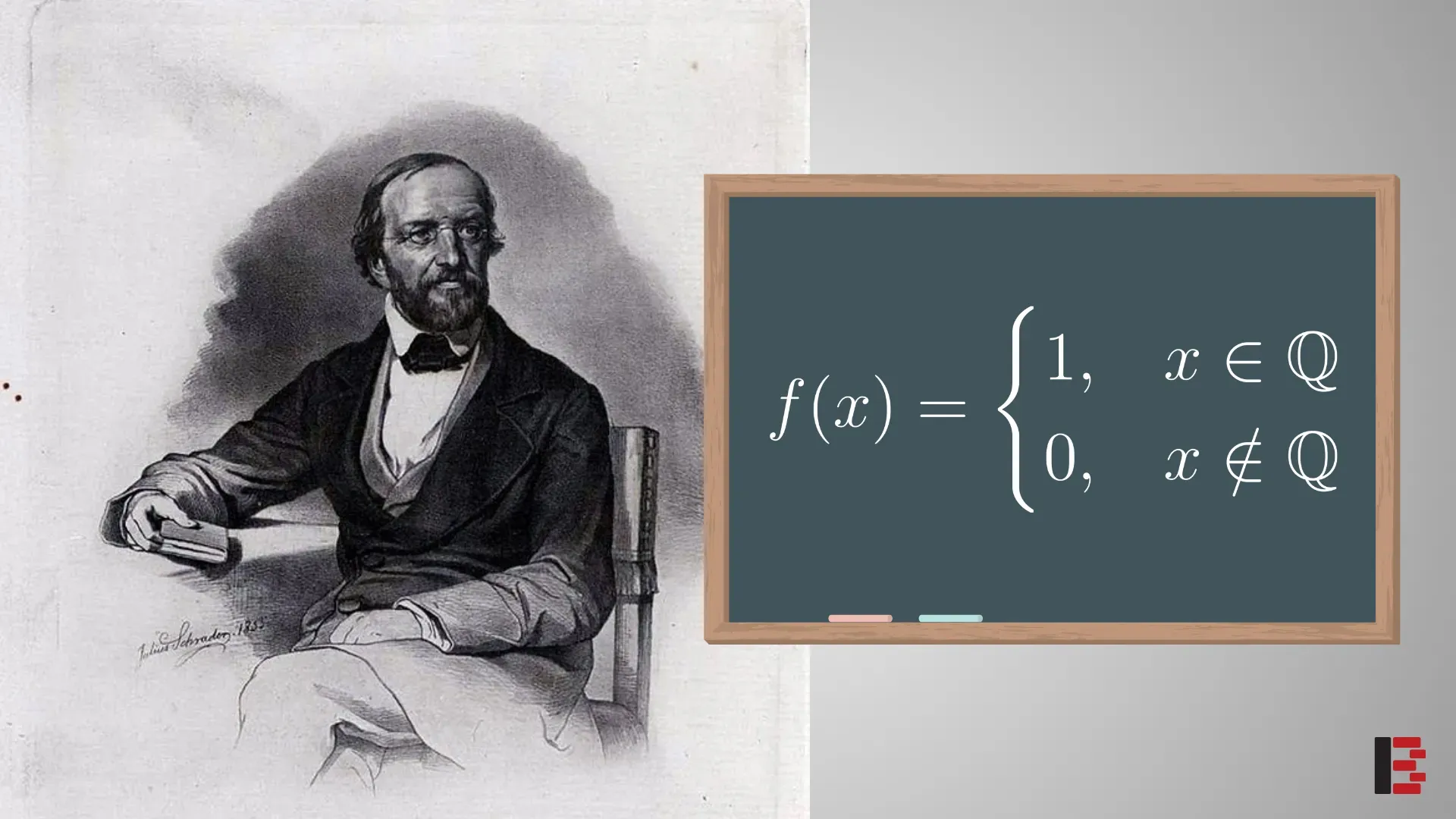Matematikte, bir fonksiyonun tanım kümesinin tüm elemanlarında süreksiz olması o kadar da ilginç bir şey değildir. Bunun o kadar ilginç olmadığını görmek için şu örneği düşünebilirsiniz: Doğal sayılar kümesinde tanımlı bir,

fonksiyonunu hayal edin. Bu fonksiyon sadece doğal sayılarda (K) tanımlı olduğundan, iki değeri arasında bir bağlantı bulunmadığı son derece açıktır ve sezgisel olarak anlaşılabilirdir. Bu da bizi bu fonksiyonun tanım kümesinde sürekli olmadığını düşünmeye iter. Peki ya tanım kümesi olarak reel sayıları (K) kabul eden bir fonksiyonun tüm tanım kümesi üzerinde süreksiz olması gibi bir ihtimal bulunabilir mi? Cevap, evet! Lakin, üstteki örneğe kıyasla bunun doğru olduğunu görmek sezgisel olarak o kadar da kolay değildir. Bu örneği göstermek için Alman matematikçi Lejeune Dirichlet tarafından bulunmuş Dirichlet Cetvel Fonksiyonu'nu inceleyeceğiz. Bu fonksiyon, Kolmak üzere:

biçiminde tanımlanır. Genellikle K olarak alınır. Fonksiyonun her reel sayıda limite sahip olmadığını ispatlamaya girişmeden önce limitin tanımına dair ufak bir hatırlatma ile işe başlayalım. Limitin teknik tanımı: "Eğer bir fonksiyonun girdisi K, K 'ya yaklaşırken değeri K civarına yaklaşıyor" demek istiyorsak bunu,

biçiminde yazarız. Bunun doğru bir ifade olabilmesi için Kfonksiyonunu K nin verilen her Kcivarında yaniK tutacak, bir K nin K civarında aralık K bulunabilmelidir. Daha salt matematiksel bir ifade ile bunu yazacak olursak: Verilen Kiçin aşağıdaki ifadeyi sağlayacak en az bir K sayısı mevcuttur.

Eğer bu ifade sağlanır ise o zaman gönül rahatlığı ile aşağıdaki ifadeyi yazabiliriz:

Şimdi bu ön hatırlatmayı hallettiğimize göre ispatımıza başlayabiliriz. Fonksiyonumuzu tekrar yazalım:

Diyelim ki Dirichlet fonksiyonumuz, K herhangi bir reel sayı olmak üzere Kiken bir limit K'ye yaklaşıyor olsun. Bu limit değeri eğer doğru ise bize verilen her Kiçin Kbulabilmeliyiz. Sözde limit Kile alakalı şunlar söylenebilir: Ya görüntü kümesinin elemanıdır yani Kya da değildir. Eğer görüntü kümesinin elemanı değilse K civarında öyle bir aralık bulunabilir ki bu aralık ne K değerini ne deK değerini içerir. Yani kısacası,

olarak alınır. Kcivarında alınacak tüm aralıklar Kdeğerini K ya da K yapacak sonsuz sayıda rasyonel ya da irrasyonel sayı içerir. Bu da fonksiyonun değerinin K'nin Kcivarının dışına çıkmasına sebep olur. Bu da limitin yanlış olduğunu gösterir. İkinci durumu inceleyelim: K görüntü kümesini bir elemanı (K) olsun. Varsayalım ki K olsun. Bu durumda ise L civarında, K'yı içermeyen bir aralık bulunabilir. Yani kısacası,

olarak alınır.K civarında K'dan yani K nin Kya uzaklığından küçük bir aralık tanımlanırsa doğal olarak bu aralık Kyı dışlamış olur. Lakin yine benzer bir şekilde Kcivarında tanımlanan her aralık için, K'in değerini K yapacak sonsuz sayıda rasyonel sayı bulunur. Bundan ötürü limit yine K olamaz. Benzer olarak K varsayıldığı durumda da geçerlidir (Bunun doğruluğu da benzer yolla ispatlanabilir.). Bu durumda herhangi bir noktada limite sahip olamayacağı gösterilmiş olur. Bu durumda süreksiz olduğu zaten sürekliliğin tamından basitçe gelir. Süreklilik,

biçiminde tanımlandığından, herhangi bir noktada limitin olmadığı fonksiyonda süreklilik kavramından bahsedilemez. Türevlenebilir bir fonksiyonun sürekli olduğu bilgisine dayanarak fonksiyonun her nokrada türevsiz olduğu bilgisi de kolayca çıkarsanabilir.

Riemann İntegrallenemezliği

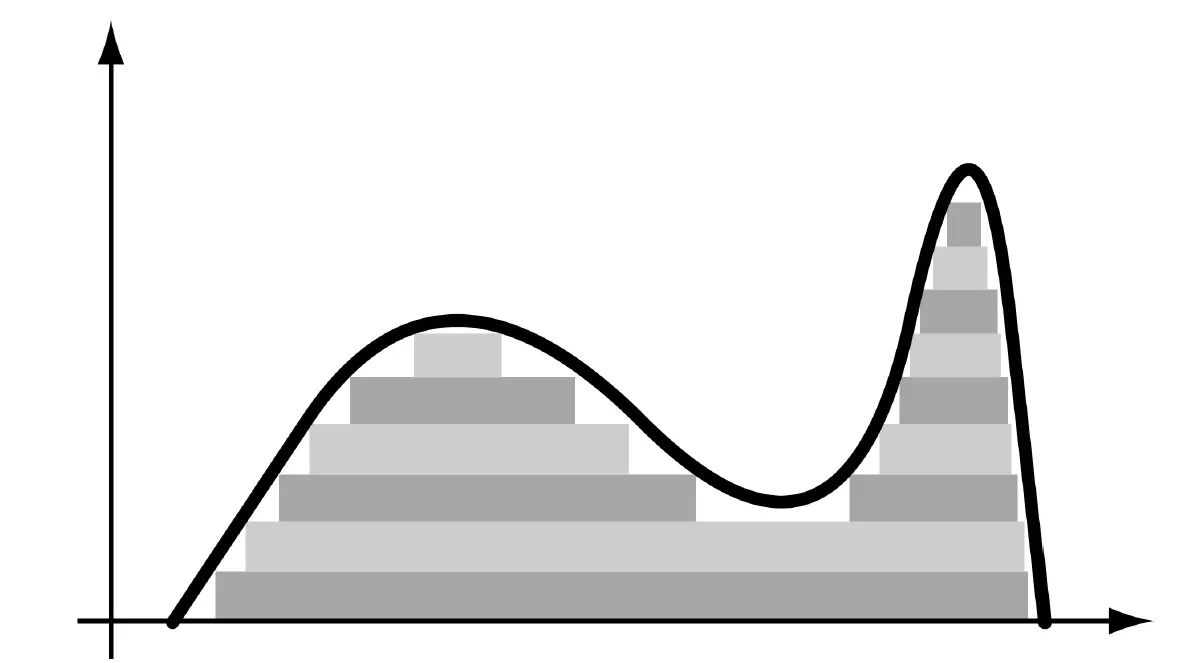
Riemann İntegrellanemezliği ismini uydurduğumuzu zannedebilirsiniz. Ancak, meşhur Thomas Kalkülüs kitabında da bu isim kullanılmaktadır. Biz de bu kullanımı beğendiğimiz için sadık kalmayı seçtik. Ne yazık ki Riemann İntegrallenemezliği'nin ispatı bu kadar basit değildir. Şu bilgiyi akılda tutarak başlayalım: Eğer bir fonksiyon Riemann integrallenebilir ise alt ve üst toplamların limiti aynı K değerine yaklaşır. Bunun bu fonksiyon için doğru olmadığı gösterilebilir ise ispat tamamlanmış olur. İşe başlamak için fonksiyonun Karalığında, herhangi birKbölünüşü (Bir aralığın parçalara ayrılmasıdır.) ile Riemann toplamı aldığımızı ve Dirichlet'in fonksiyonun değerleri için K olduğunu varsayalım (K olduğundan mutlaka biri diğerinden büyüktür.). Riemann toplamını yazıp alt ve üst toplamın değerini bulalım:

Toplam için yapılan bölünüşlerdeki aralıkların tamamı sonsuz rasyonel ve irrasyonel sayı içerir ve Kdır. Bir Riemann toplamında üst toplam değerini bulmak için o aralıktaki en büyük değeri veren noktalardan birini değerlendirmek gerekir. Bu durumda üst toplamı bulmak için herhangi bir Kdeğerini o aralıkta bulunan bir rasyonel sayı olarak almamız gerekir. Bu durumda toplamı,

olarak yazabiliriz. Eğer toplamda sabit kuralını uygularsak,

olarak yazabiliriz. Ayrıca toplamın değeri Kbölünüşündeki tüm aralıkların uzunluklarının toplamına eşit olduğundan, doğrudan aralığın uzunluğuna eşit olur. Yani, K olur. Bunu şu şekilde,

yazabiliriz. Benzer bir şekilde eğer alt toplamı bulacaksak bölünüşteki aralıklardan en küçük değeri kullanmamız gerekir. Yani, K değerini bir irrasyonel sayı olarak almamız gerekir ve benzer bir yolu izlediğimizde,

yazabiliriz. Üst toplam değeri K ve alt toplam değeri K farklı olduğundan bu fonksiyon, Riemann integrallenemezdir deriz. Burda şuna dikkat çekmek gerekir: Bir fonksiyon Riemann integrallenemez iken başka integraller ile integrallenebilir olabilir. Bu fonksiyon için Riemann integrallenemez iken Lebesgue integrallenebilirdir (yatay dikdörtgenler kullanılan integral).

ThatsMaths

İlginç Bir Özellik

Bu fonksiyon, ayrıca bize ilginç bir durumun geçerli olduğunu gösterir: İki farklı süreksiz fonksiyonun toplamı sürekli bir fonksiyona eşit olabilir. Bunu görmek için iki adet Dirichlet'in fonksiyonunu yazalım:

Hem K hem de K birer Dirichlet fonksiyonudur. Lakin K fonksiyonu rasyonel girdi için K verirken, K fonksiyonu K verir. Benzer şekilde irrasyonel girdi için K fonksiyonu K verirken, K fonksiyonu K verir. Bu fonksiyonların toplamı şuna eşittir:

Her yerde süreksiz iki fonksiyonun toplamı kısaca,

biçiminde her yerde limitli, sürekli, türevli, integrallenebilir olduğunu bildiğimiz basit bir sabit fonksiyona eşit olmuş oldu.

Çizmeye Çalışmak

Bu fonksiyon, ayrıca ilginç bir duruma daha sebebiyet vermektedir. Bunun nedenini anlamak için defterinize K eksen takımı çizin ve Dirichlet'in fonksiyonunu aşağıdaki gibi tanımlayın:

Şimdi fonksiyonun grafiğini K ile Karalığında çizmeye çalışın. Nerelerde K olması gerektiğini net olarak bulabiliyor musunuz?

Sonuç

Matematiğin etkileyici dünyasında yaptığımız bu ufak yolculukta, basit görünümüne rağmen ilginç özellikler sergileyen bir fonksiyonu inceledik. Umarım bu içeriğimizle sizi, matematiğin büyülü dünyasına biraz daha çekmeyi başarabilmişizdir.