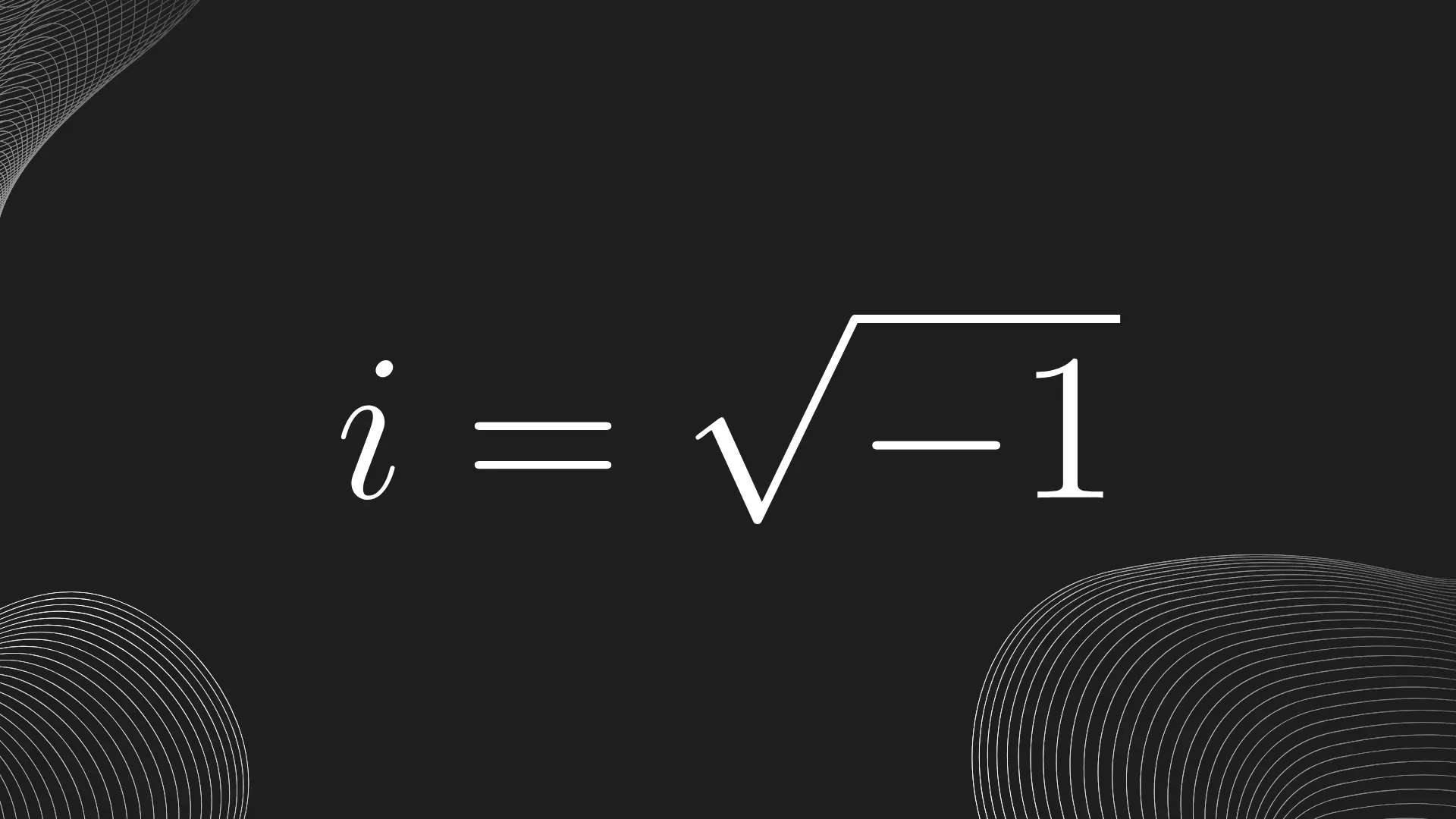Matematiğin en temel alanlarından birisi olan cebirde sıklıkla denklemler çözmemiz gerekir ve bu denklemler bizi yeni sayı kümelerine götürür. Çok basit olan tek bilinmeyenli şu denklemi ele alalım:

Bu denklemin doğal sayısının sağladığını kolaylıkla görebiliriz. Yani değeri yerine sayısının yazılması gerektiğini, 'in 'ye eşit olduğunu görebiliriz. Şimdi de şu denklemi ele alalım:

Denklemi herhangi bir doğal sayının sağlamadığını görebiliriz. Bir başka deyişle, yerine herhangi bir pozitif sayının ve sayısının gelemeyeceğini görebiliriz. Bu noktada yeni bir sayı kümesine, yani tam sayılara ihtiyaç duyarız. Sayı kümemizi genişleterek negatif sayıları, sayı kümemize ekleriz ve bu şekilde denklemi basitçe olarak çözebiliriz. yerine yazdığımızda denklem sağlanmış olur. Şimdi şu yeni denklemi ele alalım:

yerine konacak ne bir negatif ne de bir pozitif tam sayı bu denklemi sağlayamaz. Bu durum bizi, sayı kümemizin (üzerinde çalıştığımız sayıların) hâlâ yetersiz olduğu bilgisine götürür. Bu durumda tam sayıları birbirlerinin oranı olarak yazdığımız rasyonel (kesirli) sayılar kümesine () geçmemiz gerekir ve bu şekilde denklemi basitçe olarak çözebiliriz. Şimdi rasyonel sayıları da çıkmaza sokan şu denklemi ele alalım:

Konacak herhangi bir rasyonel sayının karesinin sonucunu vermediğini görmek o kadar kolay değildir ve ispatının yapmakta bu makalenin konusu olamayacak kadar uzundur. Ancak yine de bunun doğru olduğunu kabul edecek olursak yeni bir sayı türüne, yani tam sayıların oranı olarak yazılamayan sayılara veya bir başka deyişle irrasyonel sayılara ihtiyaç duyarız. Son bir adım olarak rasyonel sayılar ile irrasyonel sayılar kümesinin birleşim kümesini ele aldığımızda, gerçel (reel) sayılar kümesini () elde ederiz. Bu durumda belki artık her şeyin tamamlandığını ve herhangi bir eksik kalmadığını düşünebiliriz fakat eğer bize şu denklem verilirse, şu an bildiğimiz kümelerin bu denklemi sağlamadığını görebiliriz:

Bu denklemin sağlanabilmesi için değerinin olması gerekmektedir. Fakat değerinin anlamının 'in kendisi ile iki defa çarpılması olduğunu göz önünde bulundurduğumuzda (yani, ) denklemin neden reel sayılarda sağlanmadığı anlaşılabilir. Eğer pozitif bir sayı olsaydı, kendisi ile çarpıldığında, pozitif sayıların çarpımı da pozitif olduğundan de pozitif olurdu. Eğer negatif olsaydı, negatif sayıların çarpımı da pozitif olduğundan, yine pozitif olurdu. Bu da bize reel sayıların bu denklemi sağlamadığını gösterir. Çünkü reel sayı kümesinde kendisi ile çarpımı negatif olan bir sayı bulunmamaktadır. Bu durumda ne yapmamız gerektiği netleşiyor: Sayı kümemize kendisi ile çarpımı olan yeni bir sayı eklemeliyiz. Matematikte kendisi ile çarpımı olan sayıya "sanal birim" denir ve harfi/sembolü ile temsil edilir. Yani kısacası, yazabiliriz. Ya da buna denk olarak şeklinde de gösterebiliriz.

Bu tanımladığımız sanal sayı birimini, eğer bir katsayı ile çarparsak, ve gibi diğer sayılar da anlam kazanmaya başlar. Yani sayısını bir nevi "türetebiliriz". Örneğin şeklinde yazabiliriz çünkü eğer 'nin karesini alırsak,

biçiminde olduğunu kolaylıkla görebiliriz. Bu şekilde bir katsayı ve sanal birimin çarpımı olarak ifade edilen sayılara "yalın sanal sayı" denir. Yeni sanal birimimiz sayesinde, artık negatif kökler de bir anlam kazanmış oldu. Son adım olarak, eğer bir yalın sanal sayı ile bir reel sayıyı toplarsak karmaşık () sayılar kümesine ulaşmış oluruz. Aşağıda bir kaç karmaşık sayı örneği verilmiştir. Bu sayılar daha sade bir biçimde yazılamaz. Bu sayılar "karmaşık" ismini, zaten bir reel ve bir sanal kısımdan oluştuğundan dolayı almıştır.

Teknik olarak kompleks sayılar kümesi şu biçimde tanımlanır: Karmaşık sayılar; ve herhangi bir reel sayı ve olmak üzere, biçiminde yazılabilen sayılardır ve küme sembolü olarak gösterilir. Küme gösterimi ile,

biçiminde yazılır. Karmaşık sayıların sanal ve reel kısımlarını göstermek için iki temel notasyon mevcuttur. Bir (genelde karmaşık saylar için gösterimi yaygındır) karmaşık sayısının reel kısmını göstermek için ve sanal kısmını ( ile çarpılan kısım) göstermek için gösterimleri kullanılır. Matematiksel gösterim ile özetleyecek olursak biçiminde bir sanal sayı için aşağıdaki ifadeler yazılabilir:

Karmaşık sayılar da tıpkı reel sayılar gibi toplama, çıkarma, çarpma ve bölme gibi dört temel işleme tabi tutulabilir. Gelin şimdi bu işlemlerin nasıl tanımlandıklarını inceleyelim.

Karmaşık Sayılarla İşlemler

Karmaşık sayılarla işlemleri tanımlamak için önce iki adet karmaşık sayı tanımlayalım. Bunlar ve sayıları olsun. İki karmaşık sayının toplamı, yani , iki sayının reel ve sanal kısımlarının ayrı ayrı toplamı olarak tanımlanır. Matematiksel olarak,

şeklinde ifade edilir. Konun daha çok pekişmesi için aşağıdaki toplama örneğini inceleyebiliriz:

Karmaşık sayılarda çıkarma ise oldukça benzer bir şekilde, karşılık gelen kısımların farkı olarak tanımlanır:

Pekiştirmek için çıkarmaya da şöyle bir örnek verelim:

Karmaşık sayılarda çarpma ise aşağıdaki biçiminde tanımlanır:

İlk bakışta bu tanım oldukça anlamsız gözükebilir. Ancak temelde bu ifadeyi; çarpımının terimlerini, normal reel sayılarda olduğu gibi dağıtarak çarptığımızda elde ederiz. Dağıtma işlemini aşağıdaki örnek ile daha iyi anlayabilirsiniz:

Karmaşık sayılarda bölme ise aralarında en zor tanıma sahip olanıdır ve şu şekildedir:

Karmaşıklığı dolayısıyla bu tanımı hatırlamak biraz zor olabilir. Ancak karmaşık eşlenikleri ele aldığımız zaman, bu tanımı kullanmadan kolaylıkla bölme yapmanın bir yolunu göreceğiz. Yani endişelenmenize lüzum yok.

Karmaşık Eşlenikler

Eşlenik kavramı temelde oldukça basittir ama özellikleri incelemeye değerdir. Bir karmaşık sayısının eşleniği, sanal kısmının negatif hâlidir. Yani matematiksel olarak 'nin eşleniği sayısına eşittir. Karmaşık eşlenikleri göstermek için sayısının üzerine bir çizgi koyma notasyonu yaygındır. Kısaca 'nin eşleniğinden bahsetmek için yazılabilir. Örneğin, karmaşık sayısının eşleniği biçimdedir.

Karmaşık eşleniklerin de belirli işlem özellikleri mevcuttur. Bir ve sayısını ele alalım ve toplamlarının eşleniğini inceleyelim:

Sağdaki ifadeyi gruplayarak şu şekilde yazabiliriz:

Soldaki terimin sayısının ve sağdaki terimin sayısının eşleniği olduğuna dikkat edin. O hâlde aşağıdaki ifadeyi yazabiliriz:

Bu durumda basitçe,

ifadesinin doğru olduğuna ulaşmış olduk. Benzer şekilde çarpma ve bölme için aşağıdaki ifadeler de doğrudur ve yine tanımlardan yola çıkarak kolayca ispatlanabilir:

Eşlenikler ile ilgili en önemli özelliklerden bazıları ise bir kompleks sayıyı eşleniği ile topladığımız, çıkardığımız ve çarptığımız zaman ortaya çıkar. Yine bir sayısını ele alalım ve bu işlemlere tabii tutarak neler olduğunu inceleyelim. Öncellikle eşleniği ile toplayalım:

Bu sonuç ilginçtir çünkü bize şu formülün doğru olduğunu gösterir:

Benzer şekilde eğer eşleniğinden çıkarırsak,

sonucunu elde ederiz. Ve şu formülü yazabiliriz:

Karmaşık sayıyı eşleniği çarpmak ise,

biçiminde ilginç bir sonuç verir. Bu sonuca çarpmanın tanımından ulaşılabilir. Bu sonucun en önemli kısmı, karmaşık sayının kendisi ile çarpımının bir reel sayıya eşit olduğunu göstermesidir. Buradan elde ettiğimiz sonuç ile karmaşık sayıların bölümlerini hesaplamak için kullanışlı ve akılda tutması kolay bir yol elde edebiliriz. Eğer bir ve sayısının bölümü şeklinde ifade varsa sonucu hesaplamak için payı ve paydayı, payda da bulunan sayının eşleniği ile çarpınız. Payda kısmındaki ifade, eşlenik kuralından elde ettiğimiz şekilde,

ifadesine dönüşür. Paydaki toplam ise dağıtarak ya da çarpımının tanımı kullanılarak elde edilir:

Kesirler iki parçaya ayrılır ise tam olarak bölmenin tanımına ulaşmış oluruz:

Eşlenikleri kullanarak bölmenin tanımına daha fazla anlam yükleyebiliriz. Ayrıca bölmenin karmaşık tanımını ezberlemek yerine pay ve paydayı, paydanın eşleniği ile çarpma yöntemini uygulayabiliriz. Eşleniklerin temel faydaları bu yolla ortaya çıkmaktadır.

Sonuç

Bu makalede; karmaşık sayıların temelde ne olduklarını, küme tanımını ve işlemlerini inceledik. Karmaşık eşlenikler ve karmaşık sayıların işlem kurallarına da temel bir giriş yaptık. Karmaşık sayılar ile çalışırken sayısına sanal ya da imajiner (hayali) birim dendiğini duyabilirsiniz. Şunu bilmek önemlidir: Hayali birim sayısı da en az gerçek sayılar kadar gerçek ve gerçek sayılar kadar hayal ürünüdür. Evet, bu cümle oldukça doğru ve önemli bir cümle. Karmaşık sayılar elektronik mühendisliği, kuantum fiziği ve daha pek çok modern çağın bel kemiği olan mühendislik ve bilim dallarında son derece "gerçek" sonuçlara varmak için kullanılır. Ayrıca matematiksel denklemlerin çözümleri olarak pek çok kez karşımıza çıkarlar. Hatta bazen çözümde bir karmaşık sayı olmasa dahi, bir karmaşık sayı cebirsel bir ifadeyi çözerken işleme giden yolda belirebilir. Özetleyecek olursak karmaşık sayılar, modern çağımız için son derece gerçek ve önemli olgulardır. Umuyoruz ki bu içerik sizde karmaşık analiz konusuna karşı biraz bile olsa bir merak uyandırmıştır.