İnsanlar çağlar boyunca, sahip oldukları çoklukları kıyaslama gereği duymuşlardır. Gerek sosyal ve kültürel evrimin bir parçası olarak gerek de hayatta kalma çabasının bir ürünü olarak çokluk hesabı kaçınılmaz olmuştur. Hatta geometri bile bu sebeplerden dolayı ciddi gelişim göstermiştir.
İşte bu çoklukları ifade etmenin pek çok farklı yolu kullanılmıştır. Ancak bu çoklukları ifade etmenin yolu da matematiğin başlangıcı da sayılarla olmuştur. Tabii ki matematik her ne kadar sayılar temelli olsa da artık eskisi gibi sayısal hesaplamalardan ibaret bir saha değildir. Bundan çok daha kapsamlıdır ve hatta belki de sayısal hesaplamalar, artık eskisinden çok daha az önemlidir.
Sayıları ifade etmek için "rakam" adı verilen semboller kullanılmıştır. Bu semboller farklı zamanlarda ve kültürlerde farklı şekillerde gösterilse, çizilse de şu anda bütün dünyada genel olarak kabul edilen sayı sistemi onluk tabandır. Bu onluk tabandaki sayıları da "" rakamları ile gösteriyoruz. Yani sayıları oluşturmak için rakamları kullanıyoruz. Buradan da her sayının rakam olmadığı ama her rakamın bir sayı olduğu sonucuna varıyoruz. Yani tek başına hem bir sayı hem de bir rakamdır. Ancak, sadece bir sayıdır.
Küme Kavramı Nedir?
Sayıların sınıflandırılmasını ve sayı kümelerini anlatmadan önce kümenin ne olduğu konusunda anlaşmak gereklidir. Kümenin matematiksel anlamda bir tanımı bulunmamaktadır. Küme tanımsız bırakılmıştır ve kümeler kuramı adı verilen bir matematik sahası özel olarak kümeleri ve yapısını incelemektedir. Yani lisede öğretilen kümelerden çok (ve gerçekten çok) daha fazlası bulunmaktadır.
Bir küme, adına "öge" veya "eleman" denilen bazı nesneleri içeren bir topluluktur. Örneğin, "meyveler" bir küme oluştururlar. Hatta "sebzeler" de küme oluştururlar. Tabii bunları örnek olması amacıyla veriyoruz, bunlar matematiksel bir kümeyi ifade etmemektedir. Ancak yine de kümelerin anlaşılması için bu soyutlama yapılmış örneği vermek çok da sakıncalı değildir.
Birazdan vereceğimiz bilgi için bu ek biyoloji bilgisini bilmek gereklidir: Bütün sebzeler biyolojik olarak meyvedir. Yani salatalık da domates de aslında bilimsel olarak meyve kabul edilmektedir. Hatta sebze kavramı tek başına bilimsel olarak hiçbir anlam ifade etmemektedir. Bundan sonraki söyleyeceklerimizi bu bilimsel bilgi ışığında kurgulayacağız. Yani halk arasındaki sebze ve meyve tanımını kullanmayacağız, bilimsel olarak ele alacağız.
Yukarıdaki bilgi doğrultusunda "meyveler kümesi", "sebzeler kümesi"ni kapsar. Yani bütün meyveler sebze değildir ama bütün sebzeler meyvedir. İşte burada karşımıza "altküme" adı verilen bir kavram çıkar. Sebzeler kümesinin, meyveler kümesinin altkümesi olduğunu matematiksel olarak şu şekilde gösterebilirsiniz:
Bir de üstküme kavramı vardır ancak altküme kadar sık kullanılmaz. Bunu da yukarıdaki gösterimin tam tersi gibi düşünebilirsiniz:
Şimdi kümenin elemanlarında değinelim. Diyelim ki adında bir kümemiz var ve bu kümenin içinde "Bilimetri", "Armut" ve "Merhaba" adında üç farklı ögemiz (veya "elemanımız") var. Bu ögelerin, kümenin bir elemanı olduğunu şu şekilde gösterebiliriz:
Burada kümenin içindeki ögelerin adlarını bilerek "ilginç" seçtik çünkü kümenin içerisinde olabilecek şeylerin sadece "fiziksel" anlamda var olan şeyler olmadığını anlamanızı istiyoruz. Zira birazdan incelemeye başlayacağımız sayı kümelerinin ögelerinin hepsi soyut kavramlar olacaklar. Örneğin, sayısının fiziksel evrende hiçbir karşılığı olmayacak. Ancak, yine de binalarımızın çökmemesini sağlayacak ve binlerce kilometre uzaklıklarda uzay çalışmalarının yapılmasına yardımcı olacak. Yani soyut kavramlardan faydalanarak uygulamalı kullanımlar yapacağız ve somut sonuçlar elde edeceğiz ve bu düşündüğünüzden çok daha etkileyici bir şekilde "muazzam" işlevli bir sistemdir.
Bir de bu kümenin içerisinde yukarıda bahsettiğimiz üç ögeden başka hiçbir öge bulunmadığını varsayarsak şöyle bir matematiksel gösterim kullanabiliriz:
Burada, "Elma" ve "Kahve" ögelerinin kümesinin bir elemanı olmadığını gösterdik. Bu ifadeler doğrudur çünkü kümesi içerisinde istediğiniz kadar elma arayın ama bulamazsınız. Yine de armut bulabilirsiniz.
Boşküme, Birleşim ve Kesişim Kümesi Nelerdir?
Boşküme başlı başına çok detaylı bir konudur. Ancak bu makalenin ana konusu sayı kümeleri olduğu için detaylı bir şekilde değinmeyeceğiz. Boşküme, hiç elemanı olmayan kümedir. Boşkümenin tek bir elemanı bile bulunmamaktadır ve sembolik olarak simgesi ile gösterilir. En azından makalenin geriye kalanını daha rahat anlayabilmeniz için boşküme hakkında bu kadar bilginiz olması yeterlidir.
Birleşim kümesi ise iki veya daha çok kümede olan tüm elemanları içeren ve bunlardan başka eleman içermeyen kümedir. sembolü ile gösterilir. Örnek kümeler oluşturup bu kümelerin birleşim kümesini şu şekilde gösterebiliriz:
Görülebileceği üzere birleşim kümesi, ve kümelerindeki bütün elemanları içermektedir. Birleşim kümesini matematiksel olarak tanımlayacak olursak:
Kesişim kümesi ise iki veya daha çok kümede ortak olan elemanları içeren ve bunlardan başka eleman içermeyen kümeye denir. sembolü ile ifade edilir. Bunu da matematiksel bir örnek ile açıklayabiliriz:
Kesişim kümesi için de matematiksel bir tanım yapmamız gerekirse:
Fark Kümesi Nedir?
ve iki küme ise kümesinde olup kümesinde olmayan elemanlardan oluşan kümeye " fark kümesi" denir. ya da olarak gösterilir. Sıklıkla olarak gösterilmektedir. Bunu matematiksel olarak bir örnek ile şöyle gösterebiliriz:
Görülebileceği üzere kümesi ile kümesi farklı elemanlardan oluşmaktadır çünkü çıkarma işleminde (bunu çıkarma işlemine benzetebiliriz) yazılışın durumu sonuçta fark oluşturmaktadır.
Sayı Kümeleri
Matematikte sayıları özelliklerine göre gruplandırmak, daha rahat çalışmak ve belirli sayıların ortak özelliklerini incelemek için bazı özel kümeler tanımlanmıştır. Bu kümelere "sayı kümeleri" denmektedir. Sayı kümelerine liseden aşina olmanız olasıdır. "Sayma sayıları", "reel sayılar", "doğal sayılar" ve "kompleks sayılar" bu sayı kümelerine örnek verilebilir.
Sayma Sayıları Kümesi ()
Sayma sayıları kümesi, sayılabilir şeyler için oluşturulan bir kümedir. Sayma sayıları, bir kümenin elemanlarını azlık veya çokluk bakımından nitelemez. Sadece kümenin içinde eleman sayısını temsil eder. Türkçe matematik kaynaklarında sembolü ile gösterilse de bu uluslararası kaynaklarda pek sık görülebilecek bir gösterim değildir. Zira , kümenin isminin ilk harfinden gelmektedir. Matematik dünyasında ve akademik camiada sıklıkla sembolü ile temsil edilir.
Sayma sayılarında 0 dahil değildir. Bunun sebebi, boşküme içerisinde temsil edecek bir eleman olmamasıdır. Olmayan sayıları saymak ve temsil etmek neticesinde 0 sayısı bulunmuştur veya bir başka deyişle "uydurulmuştur". Matematik ihtiyaçlar doğrultusunda şekillenir. Yani burada bir gariplik bulunmamaktadır. Bir dönem diye bir ifadede 'e karşılık hiçbir sayı olmadığı söylenirken daha sonra negatif sayılar ortaya atılmıştır. Böylece bulunmuştur. Negatif sayıların ortaya atılmasında da borçların takibi gibi temel hayatı unsurların yer aldığı düşünülmektedir. Ya da durumunda denklemi sağlayan sayısı bulunmamaktadır denirken, ortaya sayısı atılmıştır ve karşılık bulmuştur.
Doğal Sayılar Kümesi ()
Sayma sayılarıyla (), 0'ın oluşturduğu kümeye "doğal sayılar kümesi" denmektedir. Küme sembolü ile gösterilir. Bu durumda ve gösterimleri doğrudur. Yani sayma sayıları kümesi, doğal sayılar kümesinin altkümesidir.
Doğal sayılar kümesi Peano Aksiyomları adı verilen aksiyomlar grubu ile tanımlanmaktadır. Peano Aksiyomları, dört temel ve bir yardımcı aksiyomdan oluşmaktadır. Giuseppe Peano ve Julius Wilhelm Richard Dedekind tarafından ortaya atılmıştır. Bu aksiyomlar şunlardır:
- diye bir küme vardır ve bu küme boş değildir. sayısı kümesinin bir elemanıdır ().
- kümesindeki her elemanın kendisinden başka bir ve yalnız bir tane "ardılı" vardır.
- kümesinde ardılı olan bir eleman yoktur.
- kümesinde elemanların ardılı aynı olanları birbirine eşit sayılardır.
- Bir küme 'ı içeriyorsa ve her elemanının ardılını da içeriyorsa o küme, kümesini kapsar.
Buradaki son aksiyom yardımcı bir aksiyomdur ve doğal sayılar kümesini oluşturan bir aksiyom değildir. Bu aksiyomun var olmasının sebebi tam sayılar kümesini oluşturmakta kullanılmasıdır.
Matematik dünyasında 'ın doğal sayı olup olmadığı tartışmalı ve yerine göre de değişebildiği için bu bütün aksiyomlardaki yerine de yazılabilir. Ancak biz 'ı doğal bir sayı kabul edeceğiz.
İkinci aksiyom, doğal sayıların sonsuz olduğunu göstermektedir. Doğal sayıların sonsuz olduğunu gerçekten çok basit bir ispat ile gösterebiliriz. Bu ispatta ilk defa matematikçi Öklid tarafından kullanılan olmayana ergi yolunu kullanacağız. Çok kısaca olmayana ergi yolu, bir olgunun tersini doğru kabul ederek çelişki bulmaya çalışmak üzerinedir. Yani doğal sayıların sonsuz olduğunu iddia ediyorsak, ispatı yaparken sonlu olduğunu varsayarak ilerleyeceğiz:
Varsayalım ki doğal sayılar kümesi sonlu olsun. Öyle ise bu kümedeki en büyük elemana diyelim. Doğal sayılar kümesini oluşturan Peano Aksiyomları'na göre (tanım gereği) 'in kendisinden başka yalnızca, bir ve bir tek, ardılı bulunmaktadır.
Öyle ise 'ten daha büyük bir eleman her zaman bulunabilir. Çelişki.
Burada yeri gelmişken ve sembollerinin anlamından da bahsetmek gerekir. sembolü matematiksel bir çelişki elde edildiği zaman, bu çelişkinin sonunda kullanılır. Bu sembol kullanılmadığı zaman sadece "çelişki" de yazılabilir. ise bir ispat tamamlandığı zaman ispatın sonuna çizilmektedir.
Tam Sayılar Kümesi ()
Doğal sayılar ile önlerine "" sembolü konulmuş hallerinin, yani negatif sayıların birleşimine "tam sayılar kümesi" denmektedir. Bu küme sembolü ile ifade edilmektedir. harfi, Almancada "saymak" anlamına gelen "zahlen"in baş harfinden gelmektedir.
Pozitif tam sayılar kümesi sembolü ile, negatif tam sayılar kümesi ise sembolü ile gösterilir.
Tam sayılar kümesi de doğal sayılar kümesi gibi sonsuz eleman içermektedir. Tam sayılar sıralıdır ve her sayının bir ardılı (sonraki) ve bir öncülü (önceki) vardır:
Yukarıdaki gösterimden de anlaşılabileceği gibi negatif tarafta da pozitif tarafta da sonsuz elemanı bulunmaktadır.
Rasyonel Sayılar Kümesi ()
Rasyonel sayılar kümesinin temeli kesir kavramına dayanmaktadır. Kesir kavramı matematiksel olarak şöyle gösterilmektedir:
Olmak üzere şeklinde gösterilebilen ifadelere "kesir" denmektedir. Buradaki matematiksel anlatımı biraz daha sözelleştirmemiz gerekirse; ve diye iki sayı alalım, bu sayılar tam sayılar kümesinin () elemanı olsunlar ancak elemanı sayısından farklı bir sayı olsun. Herhangi bir sayıyı, bu koşulları sağlayacak bir 'nın 'ye bölümü şeklinde gösterebiliyorsak kesirli ifadeden söz edebiliriz. Örneğin sayısı da kesirli bir ifadedir çünkü şeklinde gösterilebilir.
Değerleri aynı olan kesirlerden yalnızca bir tanesinin "temsilci" kabul edilmesi şartıyla tüm kesirler kümesine "rasyonel sayılar kümesi" denir. Değerleri aynı olan kesirlere kesri ve kesri verilebilir. İkisini de ondalık olarak gösterecek olursak 0,5 şeklinde yazabiliriz.
Bu kümeye değeri tam sayı olan kesirler de (örneğin ) gireceği için bu küme, tam sayılar kümesini kapsar. Küme, sembolü ile temsil edilmektedir. Bu sembol Almancada "oran" anlamına gelen "quote" kelimesinin baş harfinden gelmektedir. Bu sebeple bazen rasyonel sayılara "oranlı sayılar" da denmektedir.
İrrasyonel Sayılar Kümesi ()
ve için şeklinde yazılamayan sayılar da bulunmaktadır. Bu sayılara "irrasyonel sayılar" denmektedir. Örneğin, birim karenin köşegen uzunluğu karekök içerisinde sayısına eşittir ve bu sayı oransız, yani irrasyonel bir sayıdır. Aynı şekilde, bir çemberin çevre uzunluğunun, çapının uzunluğuna olan oranına eşit olan sayısı da irrasyoneldir.
İrrasyonel sayıların sembolik ifadesinde genel geçer kabul gören bir gösterim bulunmamaktadır. Kimi kaynaklarda gösterimi kullanılırken kimi kaynaklarda veya gösterimi kullanılır. Ancak şu matematiksel ifadeye rastlamak da mümkündür:
Burada anlatılan da seçeceğim bütün elemanlarının reel sayılar kümesinin bir elemanı olduğunu ve rasyonel sayılar kümesinin () kümesinin bir elemanı olmadığını göstermektedir. Yani rasyonel olmayan bütün reel sayıları kapsamaktadır.
Yukarıdaki sayıların hepsi irrasyonel sayılardır ve bir reel sayı olmalarına rağmen rasyonel sayı değillerdir.
Reel Sayılar Kümesi ()
Rasyonel sayılar kümesiyle () irrasyonel sayılar kümesinin () birleşmesiyle oluşan kümeye "reel sayılar kümesi" denmektedir. "Reel" yerine "gerçek" veya "gerçel" de denmektedir. Küme sembolü ile gösterilmektedir.
Sayı noktasındaki her bir nokta bir reel sayıyı simgelemektedir. Bu aşağıdaki aksiyomlardan gelmektedir:
Bir doğrunun noktaları ile reel sayılar öyle karşılaştırılabilir ki,
- Doğrunun her noktasına bir ve yalnız bir reel sayı karşılık gelir.
- Her reel sayıya doğrunun bir ve yalnız bir noktası denk gelir.
Reel sayılar kümesi, rasyonel sayılar kümesini ve irrasyonel sayılar kümesini kapsamaktadır. Yani herhangi bir rasyonel sayı da herhangi bir irrasyonel sayı da reel bir sayıdır.
Karmaşık Sayılar Kümesi ()
Sıfır ile sıfırın çarpımı yine sıfırdır. İki pozitif sayının da negatif sayının da kendisiyle çarpımları veya başka bir sayıyla çarpımları pozitiftir. Herhangi bir reel sayıyı kendisiyle çarparsak, yani karesini alırsak negatif bir sayı bulamayız. Fakat matematikte kendisiyle çarpımı negatif olan sayılara bir nevi bir ihtiyaç doğmuştur çünkü böyle bir sayının varlığı işleri kolaylaştırmaktadır. Bu doğrultuda karesi olan bir sayı tanımlanmıştır. Bu sayıya da denmiştir. Bu sayısına "sanal sayı birimi" denmektedir. Bu sayısı, reel sayılarla cebirsel işlemlere tabi tutularak , , , gibi yeni sayılar tanımlanmıştır.
sembolü, İngilizcede sanal anlamına gelen "imaginary" kelimesinden gelmektedir. Zaten Türkçede de "imajiner sayılar" kullanımı bulunmaktadır.
İşte bu sanal sayılar ile reel sayılar kümesinin birleşimine "karmaşık sayılar kümesi" denmektedir. Bu küme sembolü ile ifade edilmektedir. harfi, İngilizcede "karmaşık" anlamına gelen "complex" kelimesinin baş harfinden gelmektedir. Karmaşık sayılar kümesine tam olarak sanal sayılar ile reel sayıların birleşimi demek doğru olmaz. Bu kümede, hem sanal kısmı hem de reel kısmı olan özel bazı sayıların da yer aldığını belirtmek gerekir.
Karmaşık sayılar kümesi, lise müfredatında yer alan bütün sayı kümelerini kapsamaktadır. Ancak 'yi de kapsayan kümeler bulunmaktadır. Bu makalede bu kümelere değinmeyeceğiz çünkü bu kümeleri anlatmadan önce okurun belirli ileri düzey matematik konuları hakkında da bilgi sahibi olması gerekmektedir. Bu konuda daha detaylı bilgi almak için bu Bilimetri makalesini okuyabilirsiniz.
Sonuç
Sayı kümeleri, matematiksel hesaplamalar yapmak ve sayıların ortak özelliklerine yönelik çalışmalar yapmak amacıyla soyut matematikte sıklıkla kullanılmaktadır. Sayı kümeleri hakkındaki konular, bu makalede yer alanlardan çok daha fazla ve detaylıdır. Ancak temel sayı kümelerinin tamamına bu makalede değinilmiştir.
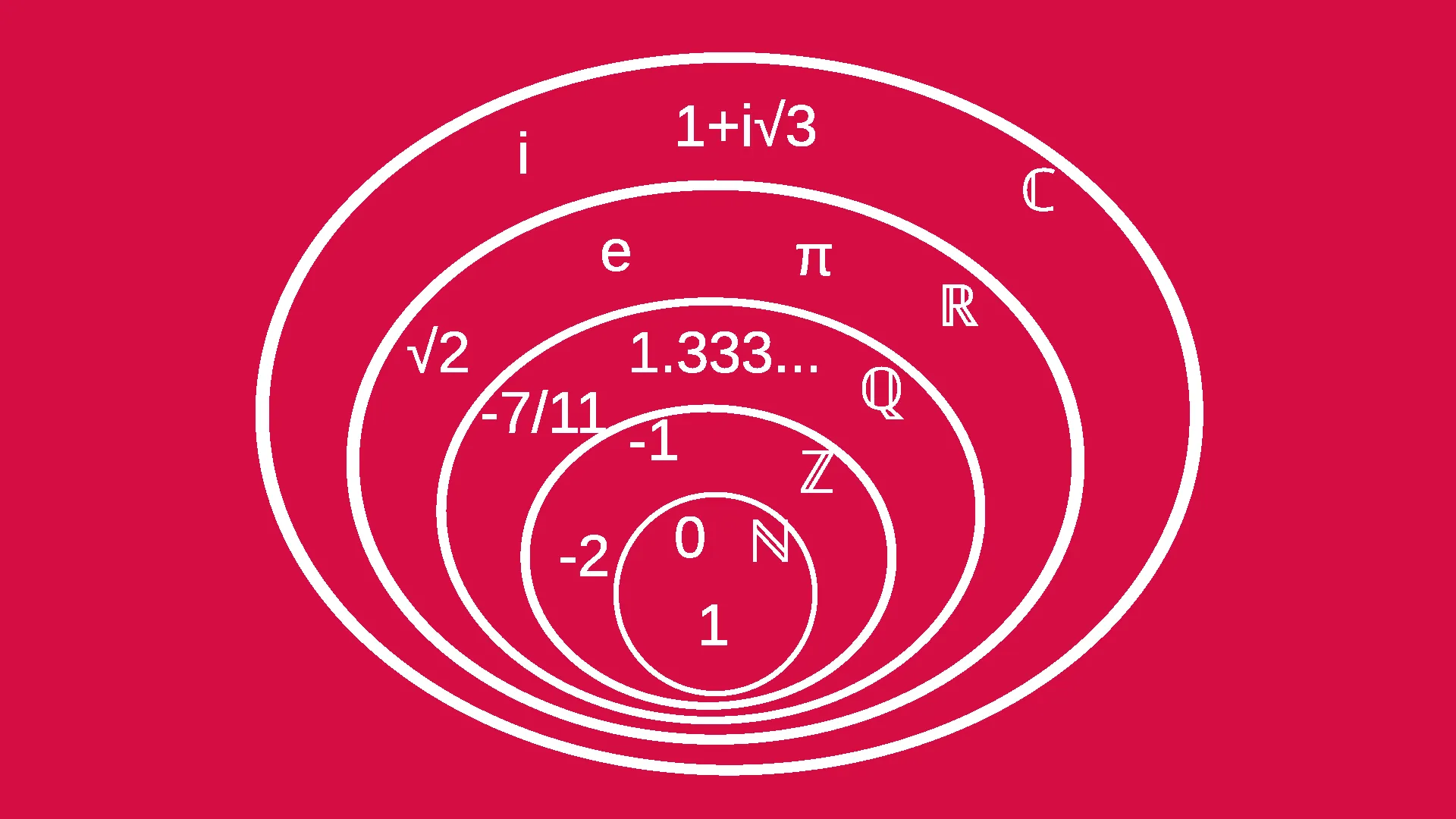
Sayı kümelerinin birbirini kapsama durumu, son hâliyle şu şekilde gösterilebilir:
Yukarıdaki gösterimi üstküme gösterimi ile de ifade etmek mümkündür:
Bu ifadelerden anlaşılabileceği gibi karmaşık sayılar kümesi, bu makalede bahsettiğimiz diğer bütün sayı kümelerini kapsamaktadır. Dolayısıyla herhangi bir sayma sayısı da herhangi bir rasyonel sayı da aynı zamanda bir karmaşık sayıdır. Ancak örneğin, herhangi bir sanal sayı hiçbir şekilde rasyonel sayılar kümesinin elemanı değildir.