Matematikte en büyük değeri bulma problemi düşünülenden daha değerli ve detaylı bir konudur. En büyük noktaları anlamak ve hesaplamak sadece soyut matematiğin bir parçası değildir. Günlük hayatta da pek çok şey bu konuyla yakından ilgilidir. Mesela bir şirketin kârını maksimize etmeye çalışması, bir çiftçinin mahsulünden maksimum verimi almaya çalışması ya da bir mühendisin bir yapının dayanabileceği en uç koşulları hesaplaması bu problem ile bağlantılıdır. Tüm bunlar maksimum yani en büyük değer veya minimum yani en küçük değerin hesaplanmasına yönelik örneklerdir.
Bu konuya basit bir giriş yapacağız ve toplamları verilen iki sayının çarpımlarının alabileceği en büyük değeri hesaplayacağız. Maksimum değerin hesaplanmasına yönelik şu teoremi ispatlayalım: Toplamları sabit olan iki sayının çarpımları, en büyük değerine sayılar birbirine eşit olduğu durumda ulaşır.
Bunu bir örnek ile daha iyi anlamaya çalışalım:
Elde ettiğimiz şey bir parabol denklemidir. Tepe noktası en yüksek olan ve benzetmek gerekirse ters U şeklinde olan bir paraboldür. Yani kolları aşağı doğru bakmaktadır.
Parabolün tepe noktası, alabileceğimiz en büyük değeri vermektedir. şeklindeki bir parabolde tepe noktası ile bulunur. Bunu yukarıdaki duruma uyarlayabiliriz:
O zaman:
Tepe noktası (c, c) olur. Bu da çarpımın alabileceği en büyük değerdir.
Bu teoremi türevden faydalanarak ispatlayabileceğimiz gibi, çok basit ve estetik bir geometrik bir yöntemle de ispatlayabiliriz:
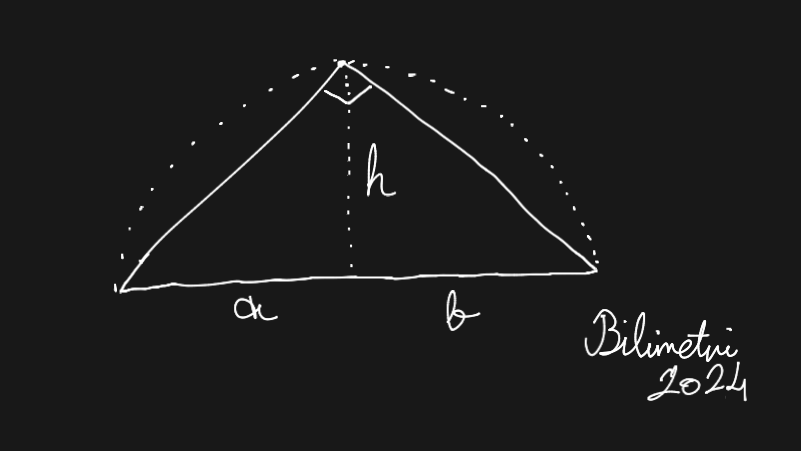
Thales'in ünlü teoremlerinden birisi bize, çapı gören çevre açının dik olduğunu söylemektedir. Bu bilgiden faydalanarak Öklid'in teoreminden de yardım alacağız. Öklid'in teoremi bilgisini bize vermektedir. en büyük değerini de en büyük değerini aldığı zaman alabilir. O yüzden durumu bize çemberin yarıçapı olan, merkezden gelen ve çember içerisinde merkezden doğrusal olarak çekebileceğimiz en uzun durumu sağlar.
Bu teorem bize pek çok sonuç çıkartır. Örneğin, çevreleri olan dikdörtgenlerden, alanı en büyük olan dikdörtgen kare olandır. Bu dikdörtgenin alanı 'dir. Bunu deneyerek test edebiliriz. dikdörtgenin çevresi, ise alanı olsun:
Bunu bir de kare olmayan bir dikdörtgen ile deneyelim ve aradaki farkı görelim. Dikdörtgenimizin uzun kenarları , kısa kenarları ise uzunluğunda olsun:
Görülebileceği üzere alan, karenin alanına kıyasla daha küçük geldi. Bu, teoremi ispatlamaya yetmez çünkü ispat için bunun her durumda geçerli olduğunun gösterilmesi gerekir. Zaten teoremin ispatını yaptığımız için bir örnek ile de test etmemizde herhangi bir sakınca bulunmuyor.
Bu teorem bize üçgenler için de yorum yapabilme olanağı sağlamaktadır. Kenarları olan üçgenlerden alanı en büyük olan üçgen eşkenar üçgendir. Yani durumudur. Hatta daha genel ve bu teoremden doğan bir teorem yazacak olursak: Çevre uzunlukları aynı olan 'genler içinde alanı en büyük olan 'gen, düzgün 'gendir. Burada , kenar sayısı temsil etmektedir. Örneğin bu sebeple, çevre uzunlukları aynı olan beşgenler arasında alanı en büyük olan düzgün beşgendir.
Şimdi buna yönelik iki farklı soruyu ele alalım. İlk sorumuz:
Olduğuna göre değeri kaçtır?
Bu soruyu şu şekilde çözebiliriz:
İkinci sorumuz:
Olduğuna göre değeri kaçtır?
Bu soruyu ise şu şekilde çözebiliriz:
Bu soruyu türevinin olduğu yere bakarak çözmek de olasıdır ama bu gereksiz ve işi uzatan bir uğraş olarak görülebilir.
Sonuç
Bu içerikte gösterilenler, toplamları verilen iki sayının çarpımlarının alabileceği en büyük değeri hesaplamaya yöneliktir. Ancak genel olarak en büyük değer hesabında bilmeniz gereken önemli bilgileri de içermektedir. Maksimum ve minimum değer hesabının derinliklerine ve türev yorumlarına geçiş yapmadan önce bu konuyu iyi bir şekilde anlamak büyük önem taşımaktadır.

